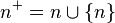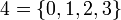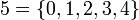Ads 468x60px

matemáticas por grados

1re grado de escuela primaria: 


la suma:
     La suma o adición es la operación básica por su naturalidad, que se combina con facilidad matemática de composición que consiste en combinar o añadir dos números o más para obtener una cantidad final o total. La suma también ilustra el proceso de juntar dos colecciones de objetos con el fin de obtener una sola colección. Por otro lado, la acción repetitiva de sumar uno es la forma más básica de contar.
     En términos más formales, la suma es una operación aritmética definida sobre conjuntos de números (naturales, enteros, racionales, reales y complejos), y también sobre estructuras asociadas a ellos, como espacios vectoriales   con vectores cuyas componentes sean estos números o funciones que tengan su imagen en ellos.
     Propiedades de la suma: 
  • Propiedad conmutativa: Si se altera el orden de los sumandos, no cambia el resultado: a+b=b+a.
  • Propiedad asociativa: Propiedad que establece que cuando se suman tres o más números reales, la suma siempre es la misma independientemente de su agrupamiento.2 Un ejemplo es: a+(b+c) = (a+b)+c.
  • Elemento neutro: 0. Para cualquier número a, a + 0 = 0 + a = a
    Como realizar la suma: 



Se procede de la siguiente manera para sumas de varios números, llamados "sumandos".



Los sumandos se colocan en filas sucesivas ordenando las cifras en columnas, empezando por la derecha con la cifra de las unidades(U), a la izquierda las decenas(D), la siguiente las centenas(C), la siguiente los millares(M), etc.
\begin{array}{rrrrr} & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline \end{array} \begin{array}{l} \\ \longleftarrow 1^{\circ} \; sumando\\ \longleftarrow 2^{\circ} \; sumando\\ \longleftarrow 3^{\circ} \; sumando\\ \end{array}
Se suman en primer lugar las cifras de la columna de las unidades según las tablas elementales, colocando en el resultado la cifra de unidades que resulte; cuando estas unidades sean más de 10 las decenas se acumulan como un sumando más en la fila de acarreo.
En este caso 3 más 9 son 12, el 2 del 12 se pone en la parte inferior y el 1 se pasa como acarreo en la columna siguiente.
\begin{array}{rrrrr} & & & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow acarreo }\\ \\ \longleftarrow 1^{\circ} \; sumando\\ \longleftarrow 2^{\circ} \; sumando\\ \longleftarrow 3^{\circ} \; sumando\\ \\ \end{array}
En la columna de las decenas, procediendo entonces a la suma de esa columna como si fueran unidades.
Sumamos el 1 del acarreo más 5, 8 y 6 que dan un total de 20, el 0 de 20 se pone en la parte inferior como resultado y el 2 se pasa como acarreo a la columna siguiente.
\begin{array}{rrrrr} & & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow acarreo }\\ \\ \longleftarrow 1^{\circ} \; sumando\\ \longleftarrow 2^{\circ} \; sumando\\ \longleftarrow 3^{\circ} \; sumando\\ \\ \end{array}
Se procede de igual forma con la columna de las decenas, acarreo incluido, colocando en la fila de acarreo sobre la columna de las centenas las decenas (de unidades de decenas).
En la columna de las centenas tenemos, el 2 de acarreo, el 7 y el 5 que sumados dan 14, el 4 del 14se pone en la parte inferior y el 1 se pasa a la siguiente columna como acarreo.
\begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow acarreo }\\ \\ \longleftarrow 1^{\circ} \; sumando\\ \longleftarrow 2^{\circ} \; sumando\\ \longleftarrow 3^{\circ} \; sumando\\ \\ \end{array}
Se procede de igual forma con todas las columnas, añadiendo a la columna última de la izquierda las decenas de la columna anterior en vez de subir a la fila de acarreo.
En la columna de los millares tenemos 1 de acareo más el 1 de sumando que sumados dan 2, que se pone en la parte inferior como resultado, al no haber mas sumandos damos por finalizada la operación.
\begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & 2 & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow acarreo }\\ \\ \longleftarrow 1^{\circ} \; sumando\\ \longleftarrow 2^{\circ} \; sumando\\ \longleftarrow 3^{\circ} \; sumando\\ \longleftarrow total\\ \end{array}


la resta
Es una de las cuatro operaciones básicas de la aritmética; se trata de una operación de descomposición que consiste en, dada cierta cantidad, eliminar una parte de ella, y el resultado se conoce como diferencia.
Es la operación inversa a la suma. Por ejemplo, si a+b=c, entonces c–b=a.
En la resta, el primer número se denomina minuendo y el segundo es el sustraendo. El resultado de la resta se denomina diferencia.
\begin{array}{rrrrr} & 1 & 1 & & \\ & M & C & D & U \\ & 1 & 4 & 1 & 9 \\ & & 7 & 5 & 1 \\ \hline & 0 & 6 & 6 & 8 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow acarreo }\\ \\ \longleftarrow \; Minuendo\\ \longleftarrow \; Sustraendo\\ \longleftarrow Resto \; o \; Diferencia\\ \end{array}
Se aplica la tabla elemental en la columna de las unidades, teniendo en cuenta que si la cifra del minuendo es menor que la del sustraendo se suma a la cifra 10 unidades, colocando en la línea de acarreo sobre las centenas un 1, que se suma a la cifra del sustraendo de las centenas, procediendo de igual forma en la columna de las unidades de millar.
La cifra 0 en el minuendo se considera como un 10, mientras que en el sustraendo no tiene ningún efecto.
números naturales
     Es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que utilizó el ser humano para contar objetos.

     Definición: 
  • La real academia española los define como "Cada uno de los elementos de la sucesión 0, 1, 2, 3..." 1
  • Es el conjunto de los umeros enteros no negativos.
  • Un numero natural es un símbolo que indica una cantidad.
El conjunto de los números naturales se representa por N y corresponde al siguiente conjunto numérico:2
\mathbb{N} = \{1, 2, 3, 4, 5, 6, 7, \dots\}
Los números naturales son un conjunto cerrado para las operaciones de la adición y la multiplicación, ya que al operar con cualquiera de sus elementos, resulta siempre un número perteneciente a N.
    El cero y la definición de los números naturales: Existe una controversia acerca de la inclusión del cero dentro del conjunto de los números naturales. De ahí que no exista acuerdo en la literatura y coexistan definiciones contradictorias de los números naturales. De hecho, algunos matemáticos (especialmente los de la teoría de  números) prefieren no reconocer el cero como un número natural; otros, especialmente los de teoría de conjuntos, lógica e informática, sostienen la postura opuesta.
Históricamente el cero no se consideraba número natural. Entre otros motivos porque no tenía una representación natural: cero dedos, cero vacas, etc. podrían considerarse puros constructos mentales.
Más recientemente, desde el punto de vista de los fundamentos lógicos de las matemáticas y de algunas aplicaciones, la situación adquirió una perspectiva nueva que hizo más natural la inclusión del cero dentro del conjunto de los números naturales. Por ejemplo, desde el punto de vista de la teoría de conjuntos, el cero se relaciona con el número de elementos del conjunto vacío. Y en informática, con un estado de la memoria en que todos los bits se encuentran en estado off.
De ahí que la inclusión del cero dentro del conjunto de los números naturales sea cuestión de contexto y de convenio, observándose una tendencia creciente a considerarlo parte de él.
     Definición de teoría de conjunto: se define al conjunto de los números naturales como el mínimo conjunto que es inductivo. La idea es que se pueda contar haciendo una biyeccion desde un número natural hasta el conjunto de objetos que se quiere contar. Es decir, para dar la definición de número 2, se requiere dar un ejemplo de un conjunto que contenga precisamente dos elementos. Esta definición fue proporcionada por Bertrand Russell, y más tarde simplificada por Von Neumann quien propuso que el candidato para 2 fuera el conjunto que contiene solo a 1 y a 0.

Formalmente, un conjunto x se dice que es un número natural si cumple
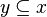
  1. Para cada y\in x, y\subseteq x
  2. La relación 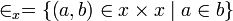\in _x = \left\{\left(a,b\right)\in x\times x \mid a\in b\right\} es un orden total estricto en x
  3. Todo subconjunto no vacío de x tiene elementos mínimo y máximo en el orden \in _x
Se intenta pues, definir un conjunto de números naturales donde cada elemento respete las convenciones anteriores. Primero se busca un conjunto que sea el representante del 0, lo cual es fácil ya que sabemos que \emptyset no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
Se define entonces que el conjunto vacío es un número natural que se denota por 0 y que cada número natural n tiene un sucesor denotado como n + . Estas ideas quedan formalizadas mediante las siguientes expresiones:
0=\emptyset
n^+=n\cup \{n\}
De esta manera, cada elemento de algún número natural es un número natural; a saber, un antecesor de él. Por ejemplo:
  • Por definición 0 = {} (lo cual refuerza el hecho de que 0 no tiene antecesores)
  • 1 es el sucesor de 0, entonces 1=0^+=\emptyset\cup\{0\}=\{0\}
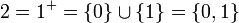
  • 2 es el sucesor de 1, pero 1 es {0}, entonces 2=1^+=\{0\}\cup\{1\}=\{0,1\}
  • y en general
3=\{0,1,2\}\,
4=\{0,1,2,3\}\,
5=\{0,1,2,3,4\}\,
\vdots
Esto permite establecer una relación de orden entre los elementos del conjunto a pesar de que un conjunto es por naturaleza un agregado de elementos desordenados. Se define esta relación mediante la expresión
a\leq b \iff a\subseteq b
es decir que un número a es menor o igual que b si y sólo si b contiene a todos los elementos de a.
También se puede usar otra definición más inmediata a partir del hecho de que cada número natural consta de sus antecesores. Así a<b\, si y sólo si a\in b.